​万有引力公式怎么推导出来（天才的直觉维维：你知道牛顿是如何推导出万有引力

万有引力公式怎么推导出来（天才的直觉维维：你知道牛顿是如何推导出万有引力定律的吗？）

当人们说艾萨克.牛顿，完全颠覆了物理学领域的时候，他们真的不是说着玩的，我们已经知道了牛顿的三大运动定律，我们可以用来描述事物如何运动，但牛顿对物理的另一个著名的贡献，是他对引力的理解。

在牛顿出生以前，科学家几乎对重力没有什么概念，他们知道当你丢东西时，物体会落在地面上，而且仔细观察他们知道行星和卫星以特定的轨道运行，他们不知道的是，这两个概念是相互关联的

当然，就像运动一样，我们现在对引力的了解，要远远比牛顿能观察到的还要多，尽管如此，当涉及到描述引力的效果时，比如说，在我们整个太阳系的规模上，牛顿的万有引力定律是不可思议的有用，这全都开始于一颗苹果。

有可能，你已经听说过牛顿和苹果的故事，故事是这样的，有一天他坐在妈妈的花园里的一棵苹果树下，树上一颗苹果掉了下来，这个时候，牛顿伟大的意识到，可能有东西拉动着苹果落向地球，这引发了另一个想法，会不会苹果也在拉动地球，但你只是看不出来呢，因为苹果对地球的作用力实在太不明显了

牛顿迸发了另一个灵感，会不会拉动苹果落向地球的相同的力，可以作用在离地球表面更远的东西上面呢，比如月球，这有点与直觉相悖，因为月球绕着地球转动，并不像树上落下的苹果，竖直的冲向地球表面。

伟大的牛顿意识到月球仍然被拉向地球，它只是侧向移动得太快，以至于一直在跑偏，这就是保持月球按轨道运动的东西，如果引力保持月球在轨道运行，那么引力对任意2个物体之间行为有什么影响呢？

比如一颗行星绕太阳旋转？不论苹果的故事，是否实际真的发生过，牛顿认为，他的想法是很有前景的，引力可能影响一切事物，包括其他行星和卫星的运行轨道，所以他开始寻找方程，能够准确的描述引力使物体运动的方式，不论是苹果落向地面，还是月球绕地球旋转，牛顿知道，不论这种引力如何产生作用，它的表现可能就会像任何其他物体所受的合力一样，它会等于物体的质量乘以物体的加速度

质量m很容易得到，这不过就是苹果的质量，或月球的质量，找出影响方程中加速度a的因素会有点困难，牛顿首先意识到，是他必须考虑的距离，当物体靠近地球表面，比如树上的苹果，引力会使物体以大约10m/s^2加速度，但月球的加速度只有下落苹果的大约1/3600，月球离地心的距离恰好同样是苹果离地心距离的大约60倍。60的平方就是3600

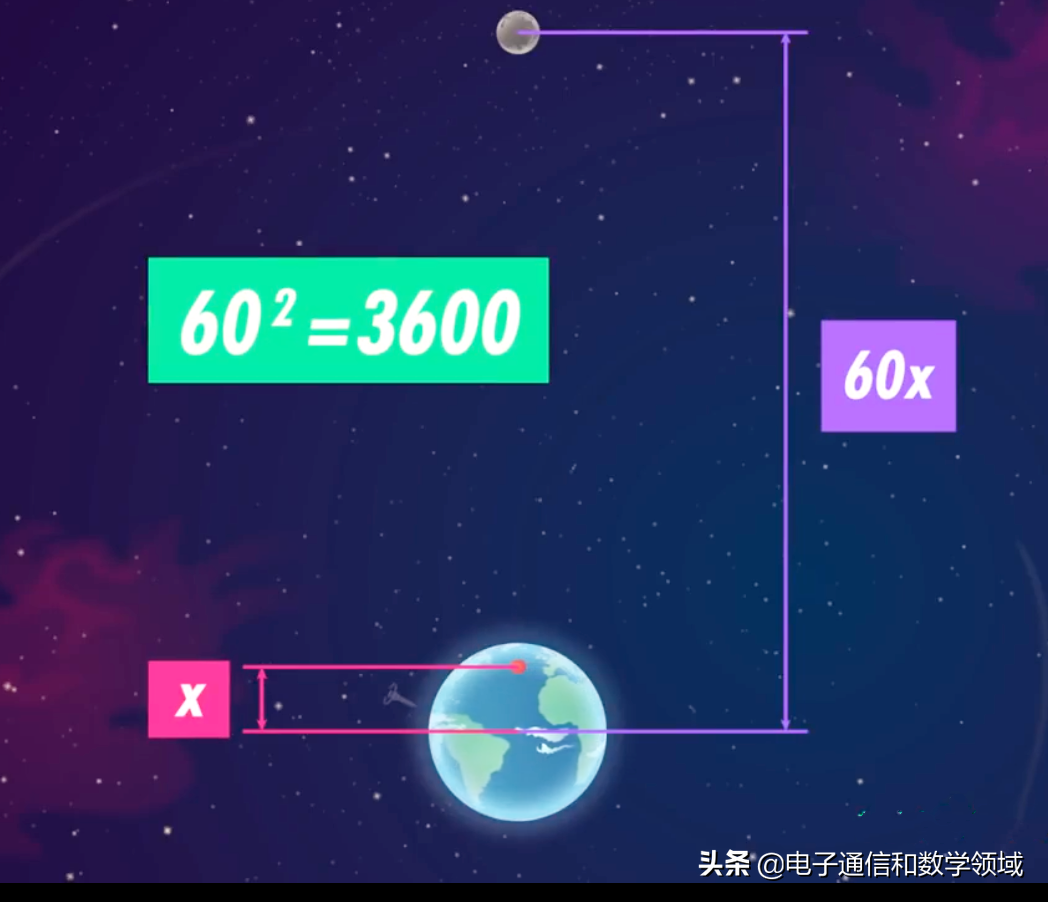
所以牛顿发现，两个物体之间引力一定随距离增大而减小，更确切的说，引力大小一定取决于两个物体距离的平方。

然后是质量，不是苹果或月球的质量，而是参与引力舞蹈中的另一个物体的质量，这个例子中，地球。牛顿意识到，两个相互拉动的物体的质量越大，它们之间的引力就越强，一旦他考虑了两个物体之间的距离，它们的质量，牛顿引力方程的大部分已经完成。

引力与两个物体质量的乘积，除以物体距离的平方，成一定的比例

但引力必须要小的多，否则，你就会看到引力会拉动日常生活中的几乎任何物体，比如，正待在原地不动的书本，而不是被拉向我，所以我和书本之间的引力一定非常小，于是牛顿在它的方程中添加了一个常数，一个非常小的数字，会使引力计算出来比原来的结果小很多，他称之为G

他称这个完整的方程

为万有引力定律，尽管牛顿当时并不知道G到底是多少，他只知道，G是一个很小的数，并把字母G放在他的方程中作为一个符号，大约100年后，亨利.卡文迪许，另一位英国物理学家，用当时最灵敏的器材进行了精密测量

他发现G大约等于

所以没错，牛对对G实际上非常小的判断是正确的，尽管他当时不知道G的确切值，伟大的牛顿已经足以建立起他的万有引力定律。

它描述了任意2个物体之间的引力，并把计算这个力的方程发表了出来